5. Inflation During French Revolution

5.1. Overview

This lecture describes some of the monetary and fiscal features of the French Revolution (1789-1799) described by [Sargent and Velde, 1995].

To finance public expenditures and service its debts, the French government embarked on policy experiments.

The authors of these experiments had in mind theories about how government monetary and fiscal policies affected economic outcomes.

Some of those theories about monetary and fiscal policies still interest us today.

• a tax-smoothing model like Robert Barro’s [Barro, 1979]

  • this normative (i.e., prescriptive model) advises a government to finance temporary war-time surges in expenditures mostly by issuing government debt, raising taxes by just enough to service the additional debt issued during the wary; then, after the war, to roll over whatever debt the government had accumulated during the war; and to increase taxes after the war permanently by just enough to finance interest payments on that post-war government debt

• unpleasant monetarist arithmetic like that described in this quanteon lecture Some Unpleasant Monetarist Arithmetic

  • mathematics involving compound interest governed French government debt dynamics in the decades preceding 1789; according to leading historians, that arithmetic set the stage for the French Revolution

• a real bills theory of the effects of government open market operations in which the government backs new issues of paper money with government holdings of valuable real property or financial assets that holders of money can purchase from the government in exchange for their money.

  • The Revolutionaries learned about this theory from Adam Smith’s 1776 book The Wealth of Nations [Smith, 2010] and other contemporary sources

  • It shaped how the Revolutionaries issued a paper money called assignats from 1789 to 1791

• a classical gold or silver standard

  • Napoleon Bonaparte became head of the French government in 1799. He used this theory to guide his monetary and fiscal policies

• a classical inflation-tax theory of inflation in which Philip Cagan’s ([Cagan, 1956]) demand for money studied in this lecture A Monetarist Theory of Price Levels is a key component

  • This theory helps explain French price level and money supply data from 1794 to 1797

• a legal restrictions or financial repression theory of the demand for real balances

  • The Twelve Members comprising the Committee of Public Safety who adminstered the Terror from June 1793 to July 1794 used this theory to shape their monetary policy

We use matplotlib to replicate several of the graphs with which [Sargent and Velde, 1995] portrayed outcomes of these experiments

5.2. Data Sources

This lecture uses data from three spreadsheets assembled by [Sargent and Velde, 1995]:

• datasets/fig_3.xlsx

• datasets/dette.xlsx

• datasets/assignat.xlsx

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams.update({'font.size': 12})

base_url = 'https://github.com/QuantEcon/lecture-python-intro/raw/'\
           + 'main/lectures/datasets/'

fig_3_url = f'{base_url}fig_3.xlsx'
dette_url = f'{base_url}dette.xlsx'
assignat_url = f'{base_url}assignat.xlsx'

5.3. Government Expenditures and Taxes Collected

We’ll start by using matplotlib to construct several graphs that will provide important historical context.

These graphs are versions of ones that appear in [Sargent and Velde, 1995].

These graphs show that during the 18th century

• government expenditures in France and Great Britain both surged during four big wars, and by comparable amounts

• In Britain, tax revenues were approximately equal to government expenditures during peace times, but were substantially less than government expenditures during wars

• In France, even in peace time, tax revenues were substantially less than government expenditures

# Read the data from Excel file
data2 = pd.read_excel(dette_url, 
        sheet_name='Militspe', usecols='M:X', 
        skiprows=7, nrows=102, header=None)

# French military spending, 1685-1789, in 1726 livres
data4 = pd.read_excel(dette_url, 
        sheet_name='Militspe', usecols='D', 
        skiprows=3, nrows=105, header=None).squeeze()
        
years = range(1685, 1790)

plt.figure()
plt.plot(years, data4, '*-', linewidth=0.8)

plt.plot(range(1689, 1791), data2.iloc[:, 4], linewidth=0.8)

plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().tick_params(labelsize=12)
plt.xlim([1689, 1790])
plt.xlabel('*: France')
plt.ylabel('Millions of livres')
plt.ylim([0, 475])

plt.tight_layout()
plt.show()

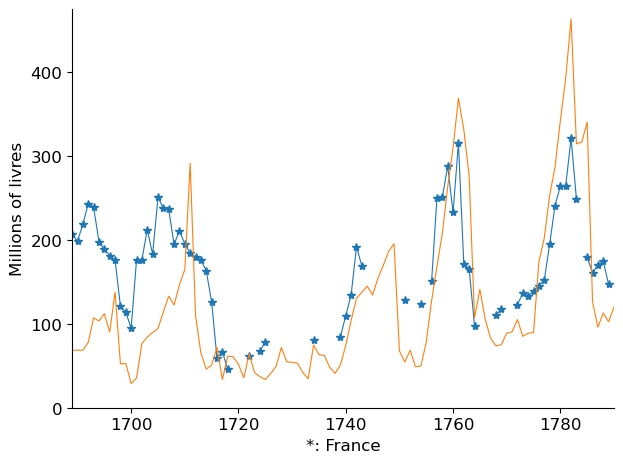
Fig. 5.1 Military Spending in Britain and France

During the 18th century, Britain and France fought four large wars.

Britain won the first three wars and lost the fourth.

Each of those wars produced surges in both countries’ government expenditures that each country somehow had to finance.

Figure Fig. 5.1 shows surges in military expenditures in France (in blue) and Great Britain. during those four wars.

A remarkable aspect of figure Fig. 5.1 is that despite having a population less than half of France’s, Britain was able to finance military expenses of about the same amounts as France’s.

This testifies to Britain’s having created state institutions that could sustain high tax collections, government spending , and government borrowing. See [North and Weingast, 1989].

# Read the data from Excel file
data2 = pd.read_excel(dette_url, sheet_name='Militspe', usecols='M:X', 
                      skiprows=7, nrows=102, header=None)

# Plot the data
plt.figure()
plt.plot(range(1689, 1791), data2.iloc[:, 5], linewidth=0.8)
plt.plot(range(1689, 1791), data2.iloc[:, 11], linewidth=0.8, color='red')
plt.plot(range(1689, 1791), data2.iloc[:, 9], linewidth=0.8, color='orange')
plt.plot(range(1689, 1791), data2.iloc[:, 8], 'o-', 
         markerfacecolor='none', linewidth=0.8, color='purple')

# Customize the plot
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().tick_params(labelsize=12)
plt.xlim([1689, 1790])
plt.ylabel('millions of pounds', fontsize=12)

# Add text annotations
plt.text(1765, 1.5, 'civil', fontsize=10)
plt.text(1760, 4.2, 'civil plus debt service', fontsize=10)
plt.text(1708, 15.5, 'total govt spending', fontsize=10)
plt.text(1759, 7.3, 'revenues', fontsize=10)

plt.tight_layout()
plt.show()

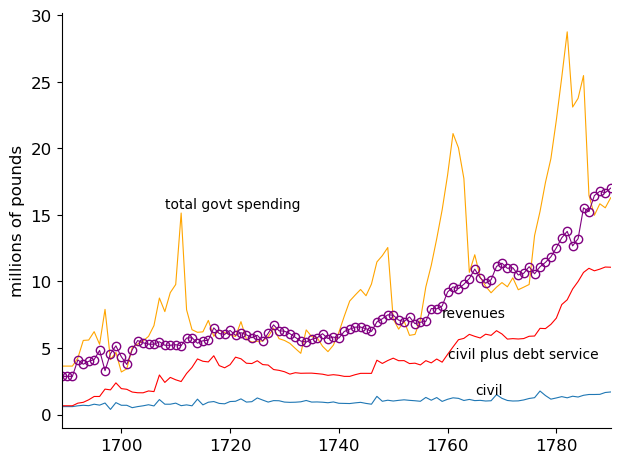
Fig. 5.2 Government Expenditures and Tax Revenues in Britain

Figures Fig. 5.2 and Fig. 5.4 summarize British and French government fiscal policies during the century before the start of the French Revolution in 1789.

Before 1789, progressive forces in France admired how Britain had financed its government expenditures and wanted to redesign French fiscal arrangements to make them more like Britain’s.

Figure Fig. 5.2 shows government expenditures and how it was distributed among expenditures for

• civil (non-military) activities

• debt service, i.e., interest payments

• military expenditures (the yellow line minus the red line)

Figure Fig. 5.2 also plots total government revenues from tax collections (the purple circled line)

Notice the surges in total government expenditures associated with surges in military expenditures in these four wars

• Wars against France’s King Louis XIV early in the 18th century

• The War of the Austrian Succession in the 1740s

• The French and Indian War in the 1750’s and 1760s

• The American War for Independence from 1775 to 1783

Figure Fig. 5.2 indicates that

• during times of peace, government expenditures approximately equal taxes and debt service payments neither grow nor decline over time

• during times of wars, government expenditures exceed tax revenues

  • the government finances the deficit of revenues relative to expenditures by issuing debt

• after a war is over, the government’s tax revenues exceed its non-interest expenditures by just enough to service the debt that the government issued to finance earlier deficits

  • thus, after a war, the government does not raise taxes by enough to pay off its debt

  • instead, it just rolls over whatever debt it inherits, raising taxes by just enough to service the interest payments on that debt

Eighteenth-century British fiscal policy portrayed Figure Fig. 5.2 thus looks very much like a text-book example of a tax-smoothing model like Robert Barro’s [Barro, 1979].

A striking feature of the graph is what we’ll label a law of gravity between tax collections and government expenditures.

• levels of government expenditures at taxes attract each other

• while they can temporarily differ – as they do during wars – they come back together when peace returns

Next we’ll plot data on debt service costs as fractions of government revenues in Great Britain and France during the 18th century.

# Read the data from the Excel file
data1 = pd.read_excel(dette_url, sheet_name='Debt', 
            usecols='R:S', skiprows=5, nrows=99, header=None)
data1a = pd.read_excel(dette_url, sheet_name='Debt', 
            usecols='P', skiprows=89, nrows=15, header=None)

# Plot the data
plt.figure()
plt.plot(range(1690, 1789), 100 * data1.iloc[:, 1], linewidth=0.8)

date = np.arange(1690, 1789)
index = (date < 1774) & (data1.iloc[:, 0] > 0)
plt.plot(date[index], 100 * data1[index].iloc[:, 0], 
         '*:', color='r', linewidth=0.8)

# Plot the additional data
plt.plot(range(1774, 1789), 100 * data1a, '*:', color='orange')

# Note about the data
# The French data before 1720 don't match up with the published version
# Set the plot properties
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().set_facecolor('white')
plt.gca().set_xlim([1688, 1788])
plt.ylabel('% of Taxes')

plt.tight_layout()
plt.show()

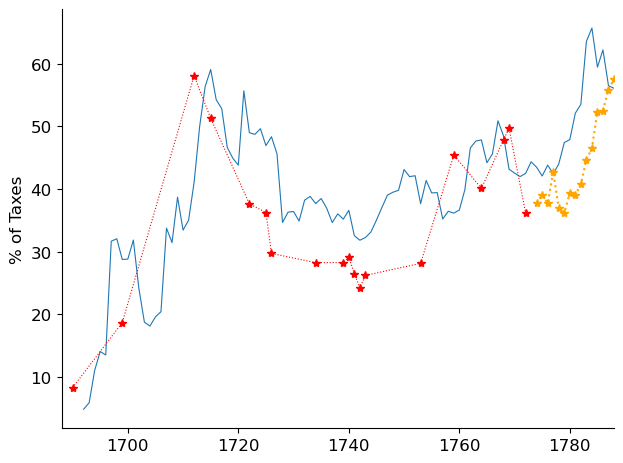
Fig. 5.3 Ratio of debt service to taxes, Britain and France

Figure Fig. 5.3 shows that interest payments on government debt (i.e., so-called ‘‘debt service’’) were high fractions of government tax revenues in both Great Britain and France.

Fig. 5.2 showed us that in peace times Britain managed to balance its budget despite those large interest costs.

But as we’ll see in our next graph, on the eve of the French Revolution in 1788, the fiscal law of gravity that worked so well in Britain did not working very well in France.

# Read the data from the Excel file
data1 = pd.read_excel(fig_3_url, sheet_name='Sheet1', 
          usecols='C:F', skiprows=5, nrows=30, header=None)

data1.replace(0, np.nan, inplace=True)

# Plot the data
plt.figure()

plt.plot(range(1759, 1789, 1), data1.iloc[:, 0], '-x', linewidth=0.8)
plt.plot(range(1759, 1789, 1), data1.iloc[:, 1], '--*', linewidth=0.8)
plt.plot(range(1759, 1789, 1), data1.iloc[:, 2], 
         '-o', linewidth=0.8, markerfacecolor='none')
plt.plot(range(1759, 1789, 1), data1.iloc[:, 3], '-*', linewidth=0.8)

plt.text(1775, 610, 'total spending', fontsize=10)
plt.text(1773, 325, 'military', fontsize=10)
plt.text(1773, 220, 'civil plus debt service', fontsize=10)
plt.text(1773, 80, 'debt service', fontsize=10)
plt.text(1785, 500, 'revenues', fontsize=10)

plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.ylim([0, 700])
plt.ylabel('millions of livres')

plt.tight_layout()
plt.show()

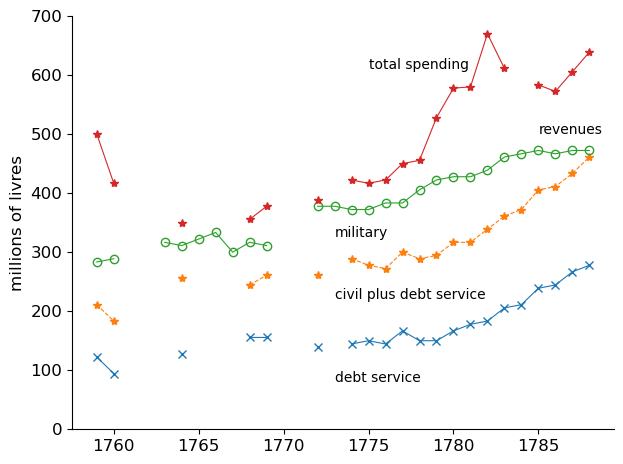
Fig. 5.4 Government Spending and Tax Revenues in France

Fig. 5.4 shows that on the eve of the French Revolution in 1788, government expenditures exceeded tax revenues.

Especially during and after France’s expenditures to help the Americans in their War of Independence from Great Britain, growing government debt service (i.e., interest payments) contributed to this situation.

This was partly a consequence of the unfolding of the debt dynamics that underlies the Unpleasant Arithmetic discussed in this quantecon lecture Some Unpleasant Monetarist Arithmetic.

[Sargent and Velde, 1995] describe how the Ancient Regime that until 1788 had governed France had stable institutional features that made it difficult for the government to balance its budget.

Powerful contending interests had prevented from the government from closing the gap between its total expenditures and its tax revenues by either

• raising taxes, or

• lowering government’s non-debt service (i.e., non-interest) expenditures, or

• lowering debt service (i.e., interest) costs by rescheduling, i.e., defaulting on some debts

Precedents and prevailing French arrangements had empowered three constituencies to block adjustments to components of the government budget constraint that they cared especially about

• tax payers

• beneficiaries of government expenditures

• government creditors (i.e., owners of government bonds)

When the French government had confronted a similar situation around 1720 after King Louis XIV’s Wars had left it with a debt crisis, it had sacrificed the interests of
government creditors, i.e., by defaulting enough of its debt to bring reduce interest payments down enough to balance the budget.

Somehow, in 1789, creditors of the French government were more powerful than they had been in 1720.

Therefore, King Louis XVI convened the Estates General together to ask them to redesign the French constitution in a way that would lower government expenditures or increase taxes, thereby allowing him to balance the budget while also honoring his promises to creditors of the French government.

The King called the Estates General together in an effort to promote the reforms that would would bring sustained budget balance.

[Sargent and Velde, 1995] describe how the French Revolutionaries set out to accomplish that.

5.4. Nationalization, Privatization, Debt Reduction

In 1789, the Revolutionaries quickly reorganized the Estates General into a National Assembly.

A first piece of business was to address the fiscal crisis, the situation that had motivated the King to convene the Estates General.

The Revolutionaries were not socialists or communists.

To the contrary, they respected private property and knew state-of-the-art economics.

They knew that to honor government debts, they would have to raise new revenues or reduce expenditures.

A coincidence was that the Catholic Church owned vast income-producing properties.

Indeed, the capitalized value of those income streams put estimates of the value of church lands at about the same amount as the entire French government debt.

This coincidence fostered a three step plan for servicing the French government debt

• nationalize the church lands – i.e., sequester or confiscate it without paying for it

• sell the church lands

• use the proceeds from those sales to service or even retire French government debt

The monetary theory underlying this plan had been set out by Adam Smith in his analysis of what he called real bills in his 1776 book The Wealth of Nations [Smith, 2010], which many of the revolutionaries had read.

Adam Smith defined a real bill as a paper money note that is backed by a claims on a real asset like productive capital or inventories.

The National Assembly put together an ingenious institutional arrangement to implement this plan.

In response to a motion by Catholic Bishop Talleyrand (an atheist), the National Assembly confiscated and nationalized Church lands.

The National Assembly intended to use earnings from Church lands to service its national debt.

To do this, it began to implement a ‘‘privatization plan’’ that would let it service its debt while not raising taxes.

Their plan involved issuing paper notes called ‘‘assignats’’ that entitled bearers to use them to purchase state lands.

These paper notes would be ‘‘as good as silver coins’’ in the sense that both were acceptable means of payment in exchange for those (formerly) church lands.

Finance Minister Necker and the Constituents of the National Assembly thus planned to solve the privatization problem and the debt problem simultaneously by creating a new currency.

They devised a scheme to raise revenues by auctioning the confiscated lands, thereby withdrawing paper notes issued on the security of the lands sold by the government.

This ‘‘tax-backed money’’ scheme propelled the National Assembly into the domains of then modern monetary theories.

Records of debates show how members of the Assembly marshaled theory and evidence to assess the likely effects of their innovation.

• Members of the National Assembly quoted David Hume and Adam Smith

• They cited John Law’s System of 1720 and the American experiences with paper money fifteen years earlier as examples of how paper money schemes can go awry

• Knowing pitfalls, they set out to avoid them

They succeeded for two or three years.

But after that, France entered a big War that disrupted the plan in ways that completely altered the character of France’s paper money. [Sargent and Velde, 1995] describe what happened.

5.5. Remaking the tax code and tax administration

In 1789 the French Revolutionaries formed a National Assembly and set out to remake French fiscal policy.

They wanted to honor government debts – interests of French government creditors were well represented in the National Assembly.

But they set out to remake the French tax code and the administrative machinery for collecting taxes.

• they abolished many taxes

• they abolished the Ancient Regimes scheme for tax farming

  • tax farming meant that the government had privatized tax collection by hiring private citizens – so-called tax farmers to collect taxes, while retaining a fraction of them as payment for their services

  • the great chemist Lavoisier was also a tax farmer, one of the reasons that the Committee for Public Safety sent him to the guillotine in 1794

As a consequence of these tax reforms, government tax revenues declined

The next figure shows this

# Read data from Excel file
data5 = pd.read_excel(dette_url, sheet_name='Debt', usecols='K', 
                    skiprows=41, nrows=120, header=None)

# Plot the data
plt.figure()
plt.plot(range(1726, 1846), data5.iloc[:, 0], linewidth=0.8)

plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().set_facecolor('white')
plt.gca().tick_params(labelsize=12)
plt.xlim([1726, 1845])
plt.ylabel('1726 = 1', fontsize=12)

plt.tight_layout()
plt.show()

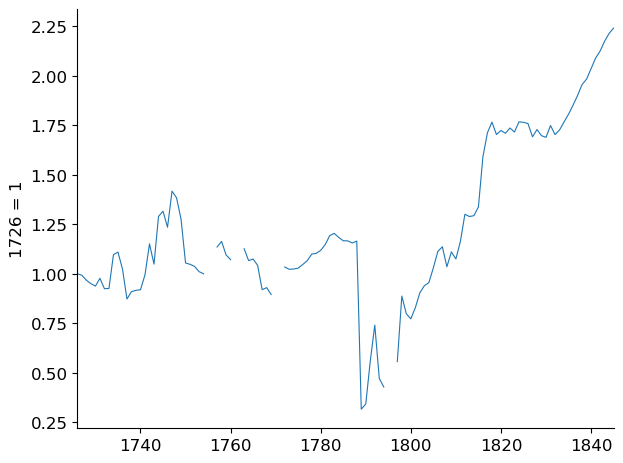
Fig. 5.5 Index of real per capital revenues, France

According to Fig. 5.5, tax revenues per capita did not rise to their pre 1789 levels until after 1815, when Napoleon Bonaparte was exiled to St Helena and King Louis XVIII was restored to the French Crown.

• from 1799 to 1814, Napoleon Bonaparte had other sources of revenues – booty and reparations from provinces and nations that he defeated in war

• from 1789 to 1799, the French Revolutionaries turned to another source to raise resources to pay for government purchases of goods and services and to service French government debt.

And as the next figure shows, government expenditures exceeded tax revenues by substantial amounts during the period form 1789 to 1799.

# Read data from Excel file
data11 = pd.read_excel(assignat_url, sheet_name='Budgets',
        usecols='J:K', skiprows=22, nrows=52, header=None)

# Prepare the x-axis data
x_data = np.concatenate([
    np.arange(1791, 1794 + 8/12, 1/12),
    np.arange(1794 + 9/12, 1795 + 3/12, 1/12)
])

# Remove NaN values from the data
data11_clean = data11.dropna()

# Plot the data
plt.figure()
h = plt.plot(x_data, data11_clean.values[:, 0], linewidth=0.8)
h = plt.plot(x_data, data11_clean.values[:, 1], '--', linewidth=0.8)

# Set plot properties
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().set_facecolor('white')
plt.gca().tick_params(axis='both', which='major', labelsize=12)
plt.xlim([1791, 1795 + 3/12])
plt.xticks(np.arange(1791, 1796))
plt.yticks(np.arange(0, 201, 20))

# Set the y-axis label
plt.ylabel('millions of livres', fontsize=12)

plt.tight_layout()
plt.show()

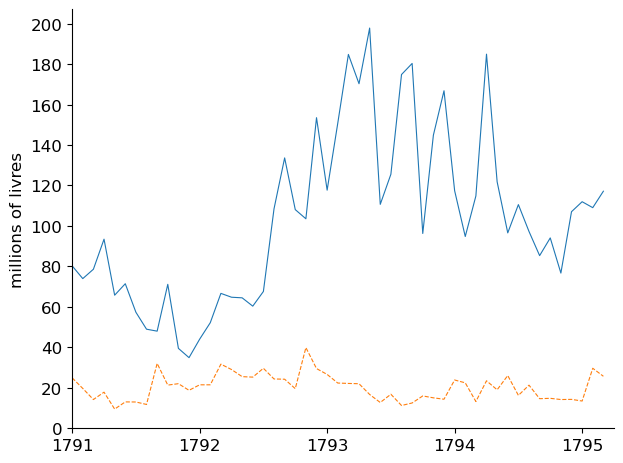
Fig. 5.6 Spending (blue) and Revenues (orange), (real values)

To cover the discrepancies between government expenditures and tax revenues revealed in Fig. 5.6, the French revolutionaries printed paper money and spent it.

The next figure shows that by printing money, they were able to finance substantial purchases of goods and services, including military goods and soldiers’ pay.

# Read data from Excel file
data12 = pd.read_excel(assignat_url, sheet_name='seignor', 
         usecols='F', skiprows=6, nrows=75, header=None).squeeze()

# Create a figure and plot the data
plt.figure()
plt.plot(pd.date_range(start='1790', periods=len(data12), freq='M'),
         data12, linewidth=0.8)

plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

plt.axhline(y=472.42/12, color='r', linestyle=':')
plt.xticks(ticks=pd.date_range(start='1790', 
           end='1796', freq='AS'), labels=range(1790, 1797))
plt.xlim(pd.Timestamp('1791'),
         pd.Timestamp('1796-02') + pd.DateOffset(months=2))
plt.ylabel('millions of livres', fontsize=12)
plt.text(pd.Timestamp('1793-11'), 39.5, 'revenues in 1788', 
         verticalalignment='top', fontsize=12)

plt.tight_layout()
plt.show()

/tmp/ipykernel_5519/529726724.py:7: FutureWarning: 'M' is deprecated and will be removed in a future version, please use 'ME' instead.
  plt.plot(pd.date_range(start='1790', periods=len(data12), freq='M'),
/tmp/ipykernel_5519/529726724.py:14: FutureWarning: 'AS' is deprecated and will be removed in a future version, please use 'YS' instead.
  plt.xticks(ticks=pd.date_range(start='1790',

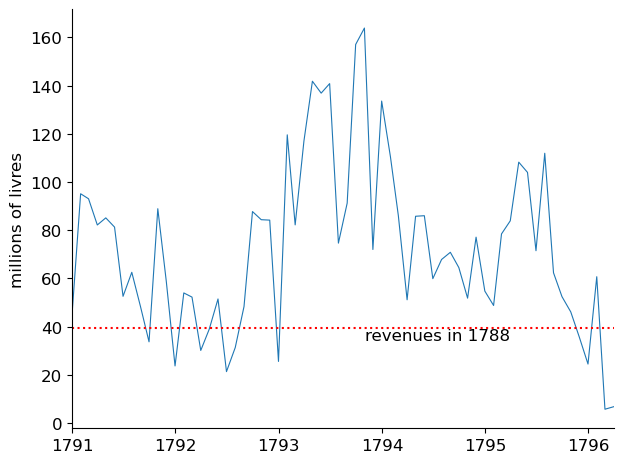
Fig. 5.7 Revenues raised by printing paper money notes

Fig. 5.7 compares the revenues raised by printing money from 1789 to 1796 with tax revenues that the Ancient Regime had raised in 1788.

Measured in goods, revenues raised at time \(t\) by printing new money equal

\[ \frac{M_{t+1} - M_t}{p_t} \]

where

• \(M_t\) is the stock of paper money at time \(t\) measured in livres

• \(p_t\) is the price level at time \(t\) measured in units of goods per livre at time \(t\)

• \(M_{t+1} - M_t\) is the amount of new money printed at time \(t\)

Notice the 1793-1794 surge in revenues raised by printing money.

• This reflects extraordinary measures that the Committee for Public Safety adopted to force citizens to accept paper money, or else.

Also note the abrupt fall off in revenues raised by 1797 and the absence of further observations after 1797.

• This reflects the end of using the printing press to raise revenues.

What French paper money entitled its holders to changed over time in interesting ways.

These led to outcomes that vary over time and that illustrate the playing out in practice of theories that guided the Revolutionaries’ monetary policy decisions.

The next figure shows the price level in France during the time that the Revolutionaries used paper money to finance parts of their expenditures.

Note that we use a log scale because the price level rose so much.

# Read the data from Excel file
data7 = pd.read_excel(assignat_url, sheet_name='Data', 
          usecols='P:Q', skiprows=4, nrows=80, header=None)
data7a = pd.read_excel(assignat_url, sheet_name='Data', 
          usecols='L', skiprows=4, nrows=80, header=None)
# Create the figure and plot
plt.figure()
x = np.arange(1789 + 10/12, 1796 + 5/12, 1/12)
h, = plt.plot(x, 1. / data7.iloc[:, 0], linestyle='--')
h, = plt.plot(x, 1. / data7.iloc[:, 1], color='r')

# Set properties of the plot
plt.gca().tick_params(labelsize=12)
plt.yscale('log')
plt.xlim([1789 + 10/12, 1796 + 5/12])
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# Add vertical lines
plt.axvline(x=1793 + 6.5/12, linestyle='-', linewidth=0.8, color='orange')
plt.axvline(x=1794 + 6.5/12, linestyle='-', linewidth=0.8, color='purple')

# Add text
plt.text(1793.75, 120, 'Terror', fontsize=12)
plt.text(1795, 2.8, 'price level', fontsize=12)
plt.text(1794.9, 40, 'gold', fontsize=12)


plt.tight_layout()
plt.show()

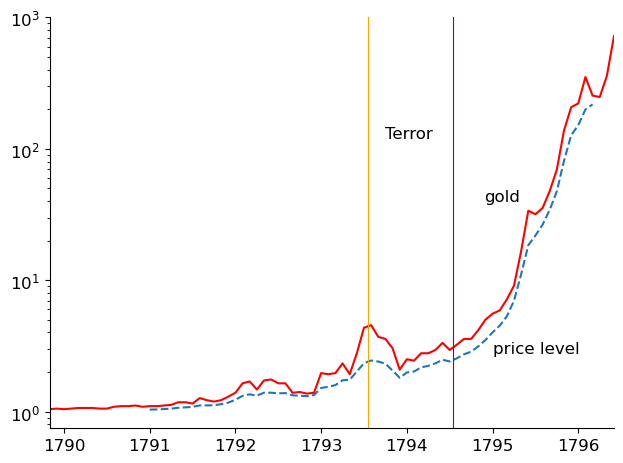
Fig. 5.8 Price Level and Price of Gold (log scale)

We have partioned Fig. 5.8 that shows the log of the price level and Fig. 5.9 below that plots real balances \(\frac{M_t}{p_t}\) into three periods that correspond to different monetary experiments or regimes.

The first period ends in the late summer of 1793, and is characterized by growing real balances and moderate inflation.

The second period begins and ends with the Terror. It is marked by high real balances, around 2,500 million, and roughly stable prices. The fall of Robespierre in late July 1794 begins the third of our episodes, in which real balances decline and prices rise rapidly.

We interpret these three episodes in terms of distinct theories

• a backing or real bills theory (the classic text for this theory is Adam Smith [Smith, 2010])

• a legal restrictions theory ( [Keynes, 1940], [Bryant and Wallace, 1984] )

• a classical hyperinflation theory ([Cagan, 1956])

Note

According to the empirical definition of hyperinflation adopted by [Cagan, 1956], beginning in the month that inflation exceeds 50 percent per month and ending in the month before inflation drops below 50 percent per month for at least a year, the assignat experienced a hyperinflation from May to December 1795.

We view these theories not as competitors but as alternative collections of ‘‘if-then’’ statements about government note issues, each of which finds its conditions more nearly met in one of these episodes than in the other two.

# Read the data from Excel file
data7 = pd.read_excel(assignat_url, sheet_name='Data', 
        usecols='P:Q', skiprows=4, nrows=80, header=None)
data7a = pd.read_excel(assignat_url, sheet_name='Data', 
        usecols='L', skiprows=4, nrows=80, header=None)

# Create the figure and plot
plt.figure()
h = plt.plot(pd.date_range(start='1789-11-01', periods=len(data7), freq='M'), 
            (data7a.values * [1, 1]) * data7.values, linewidth=1.)
plt.setp(h[1], linestyle='--', color='red')

plt.vlines([pd.Timestamp('1793-07-15'), pd.Timestamp('1793-07-15')], 
           0, 3000, linewidth=0.8, color='orange')
plt.vlines([pd.Timestamp('1794-07-15'), pd.Timestamp('1794-07-15')], 
           0, 3000, linewidth=0.8, color='purple')

plt.ylim([0, 3000])

# Set properties of the plot
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().set_facecolor('white')
plt.gca().tick_params(labelsize=12)
plt.xlim(pd.Timestamp('1789-11-01'), pd.Timestamp('1796-06-01'))
plt.ylabel('millions of livres', fontsize=12)

# Add text annotations
plt.text(pd.Timestamp('1793-09-01'), 200, 'Terror', fontsize=12)
plt.text(pd.Timestamp('1791-05-01'), 750, 'gold value', fontsize=12)
plt.text(pd.Timestamp('1794-10-01'), 2500, 'real value', fontsize=12)


plt.tight_layout()
plt.show()

/tmp/ipykernel_5519/4102237171.py:9: FutureWarning: 'M' is deprecated and will be removed in a future version, please use 'ME' instead.
  h = plt.plot(pd.date_range(start='1789-11-01', periods=len(data7), freq='M'),

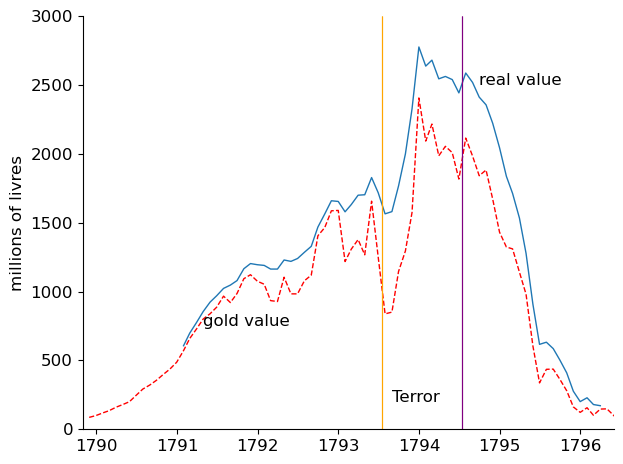
Fig. 5.9 Real balances of assignats (in gold and goods)

The three clouds of points in Figure Fig. 5.10 depict different real balance-inflation relationships.

Only the cloud for the third period has the inverse relationship familiar to us now from twentieth-century hyperinflations.

• subperiod 1: (”real bills period): January 1791 to July 1793

• subperiod 2: (“terror”): August 1793 - July 1794

• subperiod 3: (“classic Cagan hyperinflation”): August 1794 - March 1796

def fit(x, y):

    b = np.cov(x, y)[0, 1] / np.var(x)
    a = y.mean() - b * x.mean()

    return a, b

# Load data
caron = np.load('datasets/caron.npy')
nom_balances = np.load('datasets/nom_balances.npy')

infl = np.concatenate(([np.nan], 
      -np.log(caron[1:63, 1] / caron[0:62, 1])))
bal = nom_balances[14:77, 1] * caron[:, 1] / 1000

# Regress y on x for three periods
a1, b1 = fit(bal[1:31], infl[1:31])
a2, b2 = fit(bal[31:44], infl[31:44])
a3, b3 = fit(bal[44:63], infl[44:63])

# Regress x on y for three periods
a1_rev, b1_rev = fit(infl[1:31], bal[1:31])
a2_rev, b2_rev = fit(infl[31:44], bal[31:44])
a3_rev, b3_rev = fit(infl[44:63], bal[44:63])

plt.figure()
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# First subsample
plt.plot(bal[1:31], infl[1:31], 'o', markerfacecolor='none', 
         color='blue', label='real bills period')

# Second subsample
plt.plot(bal[31:44], infl[31:44], '+', color='red', label='terror')

# Third subsample
plt.plot(bal[44:63], infl[44:63], '*', 
        color='orange', label='classic Cagan hyperinflation')

plt.xlabel('real balances')
plt.ylabel('inflation')
plt.legend()

plt.tight_layout()
plt.show()

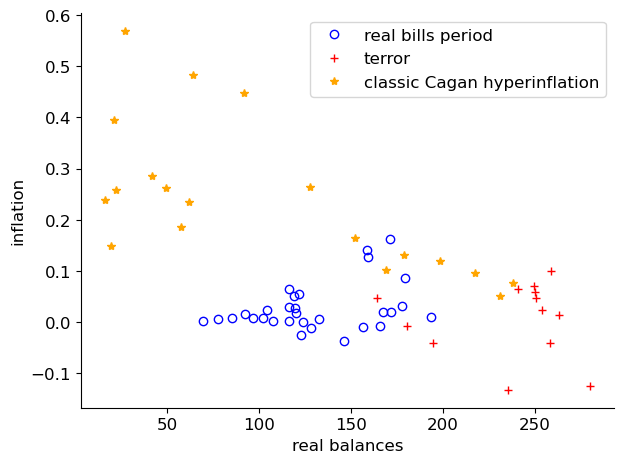
Fig. 5.10 Inflation and Real Balances

The three clouds of points in Fig. 5.10 evidently depict different real balance-inflation relationships.

Only the cloud for the third period has the inverse relationship familiar to us now from twentieth-century hyperinflations.

To bring this out, we’ll use linear regressions to draw straight lines that compress the inflation-real balance relationship for our three sub-periods.

Before we do that, we’ll drop some of the early observations during the terror period to obtain the following graph.

# Regress y on x for three periods
a1, b1 = fit(bal[1:31], infl[1:31])
a2, b2 = fit(bal[31:44], infl[31:44])
a3, b3 = fit(bal[44:63], infl[44:63])

# Regress x on y for three periods
a1_rev, b1_rev = fit(infl[1:31], bal[1:31])
a2_rev, b2_rev = fit(infl[31:44], bal[31:44])
a3_rev, b3_rev = fit(infl[44:63], bal[44:63])

plt.figure()
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# First subsample
plt.plot(bal[1:31], infl[1:31], 'o', markerfacecolor='none', color='blue', label='real bills period')

# Second subsample
plt.plot(bal[34:44], infl[34:44], '+', color='red', label='terror')

# Third subsample
plt.plot(bal[44:63], infl[44:63], '*', color='orange', label='classic Cagan hyperinflation')

plt.xlabel('real balances')
plt.ylabel('inflation')
plt.legend()

plt.tight_layout()
plt.show()

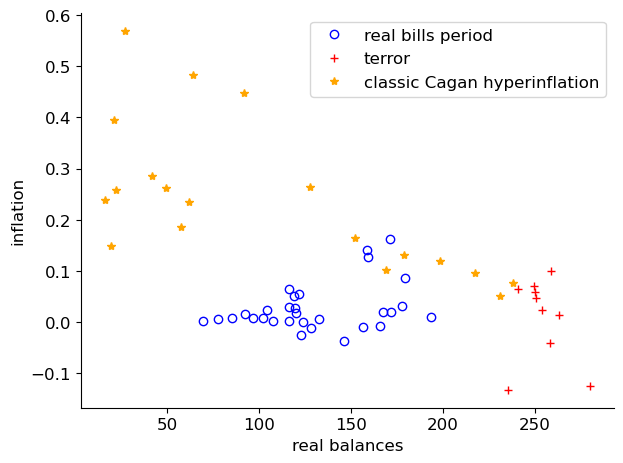
Fig. 5.11 Inflation and Real Balances

Now let’s regress inflation on real balances during the real bills period and plot the regression line.

plt.figure()
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# First subsample
plt.plot(bal[1:31], infl[1:31], 'o', markerfacecolor='none', 
        color='blue', label='real bills period')
plt.plot(bal[1:31], a1 + bal[1:31] * b1, color='blue')

# Second subsample
plt.plot(bal[31:44], infl[31:44], '+', color='red', label='terror')

# Third subsample
plt.plot(bal[44:63], infl[44:63], '*', 
        color='orange', label='classic Cagan hyperinflation')

plt.xlabel('real balances')
plt.ylabel('inflation')
plt.legend()

plt.tight_layout()
plt.show()

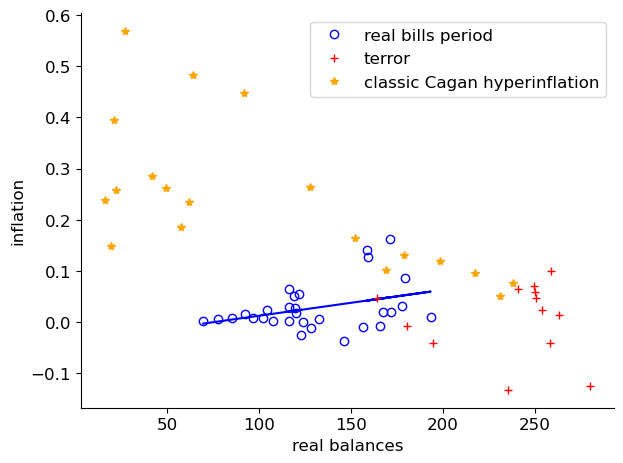
Fig. 5.12 Inflation and Real Balances

The regression line in Fig. 5.12 shows that large increases in real balances of assignats (paper money) were accompanied by only modest rises in the price level, an outcome in line with the real bills theory.

During this period, assignats were claims on church lands.

But towards the end of this period, the price level started to rise and real balances to fall as the government continued to print money but stopped selling church land.

To get people to hold that paper money, the government forced people to hold it by using legal restrictions.

Now let’s regress real balances on inflation during the terror and plot the regression line.

plt.figure()
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# First subsample
plt.plot(bal[1:31], infl[1:31], 'o', markerfacecolor='none', 
        color='blue', label='real bills period')

# Second subsample
plt.plot(bal[31:44], infl[31:44], '+', color='red', label='terror')
plt.plot(a2_rev + b2_rev * infl[31:44], infl[31:44], color='red')

# Third subsample
plt.plot(bal[44:63], infl[44:63], '*', 
        color='orange', label='classic Cagan hyperinflation')

plt.xlabel('real balances')
plt.ylabel('inflation')
plt.legend()

plt.tight_layout()
plt.show()

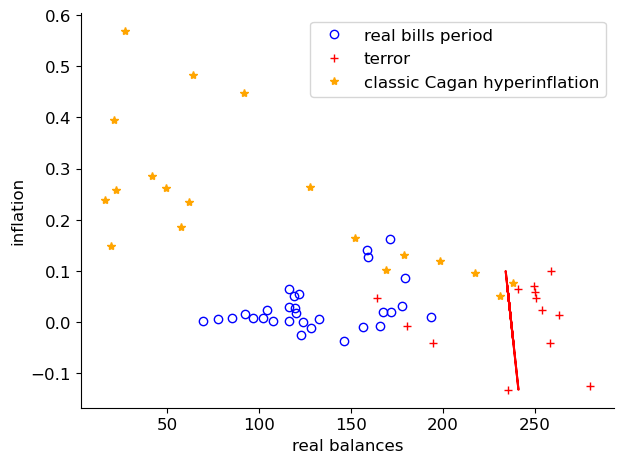
Fig. 5.13 Inflation and Real Balances

The regression line in Fig. 5.13 shows that large increases in real balances of assignats (paper money) were accompanied by little upward price level pressure, even some declines in prices.

This reflects how well legal restrictions – financial repression – was working during the period of the Terror.

But the Terror ended in July 1794. That unleashed a big inflation as people tried to find other ways to transact and store values.

The following two graphs are for the classical hyperinflation period.

One regresses inflation on real balances, the other regresses real balances on inflation.

Both show a prounced inverse relationship that is the hallmark of the hyperinflations studied by Cagan [Cagan, 1956].

plt.figure()
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# First subsample
plt.plot(bal[1:31], infl[1:31], 'o', markerfacecolor='none', 
        color='blue', label='real bills period')

# Second subsample
plt.plot(bal[31:44], infl[31:44], '+', color='red', label='terror')

# Third subsample
plt.plot(bal[44:63], infl[44:63], '*', 
    color='orange', label='classic Cagan hyperinflation')
plt.plot(bal[44:63], a3 + bal[44:63] * b3, color='orange')

plt.xlabel('real balances')
plt.ylabel('inflation')
plt.legend()

plt.tight_layout()
plt.show()

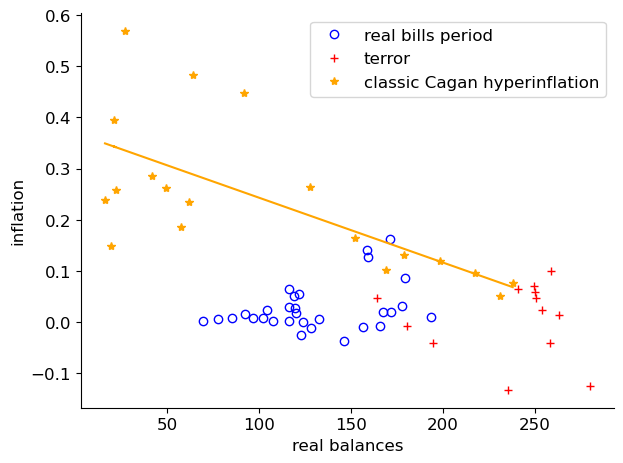
Fig. 5.14 Inflation and Real Balances

Fig. 5.14 shows the results of regressing inflation on real balances during the period of the hyperinflation.

plt.figure()
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

# First subsample
plt.plot(bal[1:31], infl[1:31], 'o', 
    markerfacecolor='none', color='blue', label='real bills period')

# Second subsample
plt.plot(bal[31:44], infl[31:44], '+', color='red', label='terror')

# Third subsample
plt.plot(bal[44:63], infl[44:63], '*', 
        color='orange', label='classic Cagan hyperinflation')
plt.plot(a3_rev + b3_rev * infl[44:63], infl[44:63], color='orange')

plt.xlabel('real balances')
plt.ylabel('inflation')
plt.legend()

plt.tight_layout()
plt.show()

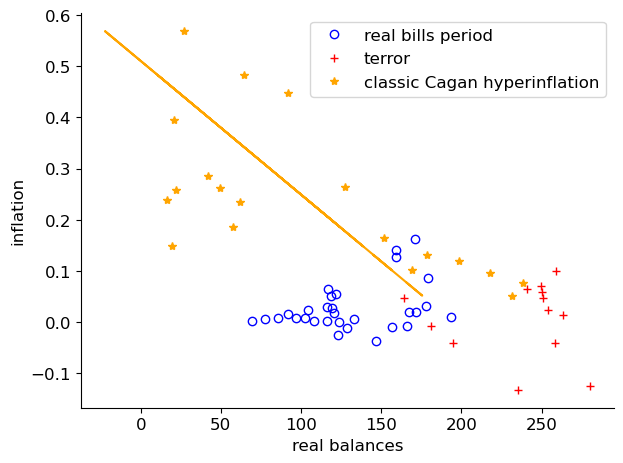
Fig. 5.15 Inflation and Real Balances

Fig. 5.14 shows the results of regressing real money balances on inflation during the period of the hyperinflation.

5.6. Hyperinflation Ends

[Sargent and Velde, 1995] tell how in 1797 the Revolutionary government abruptly ended the inflation by

• repudiating 2/3 of the national debt, and thereby

• eliminating the net-of-interest government defict

• no longer printing money, but instead

• using gold and silver coins as money

In 1799, Napoleon Bonaparte became first consul and for the next 15 years used resources confiscated from conquered territories to help pay for French government expenditures.

5.7. Underlying Theories

This lecture sets the stage for studying theories of inflation and the government monetary and fiscal policies that bring it about.

A monetarist theory of the price level is described in this quantecon lecture A Monetarist Theory of Price Levels.

That lecture sets the stage for these quantecon lectures Money Financed Government Deficits and Price Levels and Some Unpleasant Monetarist Arithmetic.