36. Linear Programming#

In this lecture, we will need the following library. Install ortools using pip.

!pip install ortools
Hide code cell output 
Collecting ortools

  Downloading ortools-9.11.4210-cp312-cp312-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata (3.0 kB)
Collecting absl-py>=2.0.0 (from ortools)
  Downloading absl_py-2.1.0-py3-none-any.whl.metadata (2.3 kB)
Requirement already satisfied: numpy>=1.13.3 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from ortools) (1.26.4)
Requirement already satisfied: pandas>=2.0.0 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from ortools) (2.2.2)

Collecting protobuf<5.27,>=5.26.1 (from ortools)
  Downloading protobuf-5.26.1-cp37-abi3-manylinux2014_x86_64.whl.metadata (592 bytes)
Collecting immutabledict>=3.0.0 (from ortools)
  Downloading immutabledict-4.2.1-py3-none-any.whl.metadata (3.5 kB)

Requirement already satisfied: python-dateutil>=2.8.2 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from pandas>=2.0.0->ortools) (2.9.0.post0)
Requirement already satisfied: pytz>=2020.1 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from pandas>=2.0.0->ortools) (2024.1)
Requirement already satisfied: tzdata>=2022.7 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from pandas>=2.0.0->ortools) (2023.3)
Requirement already satisfied: six>=1.5 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from python-dateutil>=2.8.2->pandas>=2.0.0->ortools) (1.16.0)
Downloading ortools-9.11.4210-cp312-cp312-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (28.1 MB)
?25l   ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/28.1 MB ? eta -:--:--

   ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 28.1/28.1 MB 155.6 MB/s eta 0:00:00
?25hDownloading absl_py-2.1.0-py3-none-any.whl (133 kB)
Downloading immutabledict-4.2.1-py3-none-any.whl (4.7 kB)
Downloading protobuf-5.26.1-cp37-abi3-manylinux2014_x86_64.whl (302 kB)

Installing collected packages: protobuf, immutabledict, absl-py, ortools
  Attempting uninstall: protobuf

    Found existing installation: protobuf 4.25.3
    Uninstalling protobuf-4.25.3:

      Successfully uninstalled protobuf-4.25.3

Successfully installed absl-py-2.1.0 immutabledict-4.2.1 ortools-9.11.4210 protobuf-5.26.1

36.1. Overview#

Linear programming problems either maximize or minimize a linear objective function subject to a set of linear equality and/or inequality constraints.

Linear programs come in pairs:

  • an original primal problem, and

  • an associated dual problem.

If a primal problem involves maximization, the dual problem involves minimization.

If a primal problem involves minimization*, the dual problem involves *maximization.

We provide a standard form of a linear program and methods to transform other forms of linear programming problems into a standard form.

We tell how to solve a linear programming problem using SciPy and Google OR-Tools.

See also

In another lecture, we will employ the linear programming method to solve the optimal transport problem.

Let’s start with some standard imports.

import numpy as np
from ortools.linear_solver import pywraplp
from scipy.optimize import linprog
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon

Let’s start with some examples of linear programming problem.

36.2. Example 1: production problem#

This example was created by [Bertsimas, 1997]

Suppose that a factory can produce two goods called Product \(1\) and Product \(2\).

To produce each product requires both material and labor.

Selling each product generates revenue.

Required per unit material and labor inputs and revenues are shown in table below:

Product 1

Product 2

Material

2

5

Labor

4

2

Revenue

3

4

30 units of material and 20 units of labor available.

A firm’s problem is to construct a production plan that uses its 30 units of materials and 20 units of labor to maximize its revenue.

Let \(x_i\) denote the quantity of Product \(i\) that the firm produces and \(z\) denote the total revenue.

This problem can be formulated as:

\[\begin{split} \begin{aligned} \max_{x_1,x_2} \ & z = 3 x_1 + 4 x_2 \\ \mbox{subject to } \ & 2 x_1 + 5 x_2 \le 30 \\ & 4 x_1 + 2 x_2 \le 20 \\ & x_1, x_2 \ge 0 \\ \end{aligned} \end{split}\]

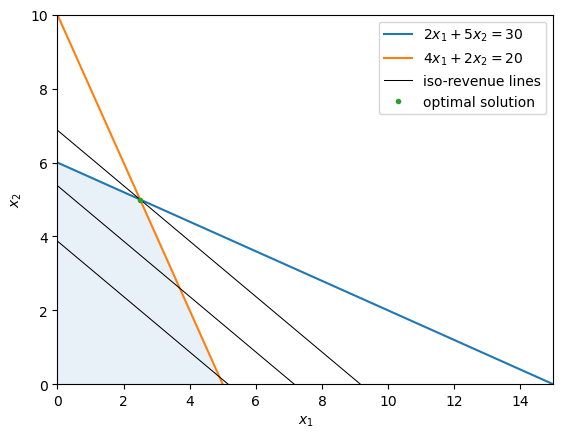
The following graph illustrates the firm’s constraints and iso-revenue lines.

Iso-revenue lines show all the combinations of materials and labor that produce the same revenue.

Hide code cell source 
fig, ax = plt.subplots()
# Draw constraint lines
ax.set_xlim(0,15)
ax.set_ylim(0,10)
x1 = np.linspace(0, 15)
ax.plot(x1, 6-0.4*x1, label="$2x_1 + 5x_2=30$")
ax.plot(x1, 10-2*x1, label="$4x_1 + 2x_2=20$")


# Draw the feasible region
feasible_set = Polygon(np.array([[0, 0],[0, 6],[2.5, 5],[5, 0]]), alpha=0.1)
ax.add_patch(feasible_set)

# Draw the objective function
ax.plot(x1, 3.875-0.75*x1, label="iso-revenue lines",color='k',linewidth=0.75)
ax.plot(x1, 5.375-0.75*x1, color='k',linewidth=0.75)
ax.plot(x1, 6.875-0.75*x1, color='k',linewidth=0.75)

# Draw the optimal solution
ax.plot(2.5, 5, ".", label="optimal solution")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.legend()

plt.show()
_images/888f6fa7457c0868ffc6912ab6182da13d5ad2db105a1af8903ad46fecabe149.png

The blue region is the feasible set within which all constraints are satisfied.

Parallel black lines are iso-revenue lines.

The firm’s objective is to find the parallel black lines to the upper boundary of the feasible set.

The intersection of the feasible set and the highest black line delineates the optimal set.

In this example, the optimal set is the point \((2.5, 5)\).

36.2.1. Computation: using OR-Tools#

Let’s try to solve the same problem using the package ortools.linear_solver.

The following cell instantiates a solver and creates two variables specifying the range of values that they can have.

# Instantiate a GLOP(Google Linear Optimization Package) solver
solver = pywraplp.Solver.CreateSolver('GLOP')

Let’s create two variables \(x_1\) and \(x_2\) such that they can only have nonnegative values.

# Create the two variables and let them take on any non-negative value.
x1 = solver.NumVar(0, solver.infinity(), 'x1')
x2 = solver.NumVar(0, solver.infinity(), 'x2')

Add the constraints to the problem.

# Constraint 1: 2x_1 + 5x_2 <= 30.0
solver.Add(2 * x1 + 5 * x2 <= 30.0)

# Constraint 2: 4x_1 + 2x_2 <= 20.0
solver.Add(4 * x1 + 2 * x2 <= 20.0)

<ortools.linear_solver.pywraplp.Constraint; proxy of <Swig Object of type 'operations_research::MPConstraint *' at 0x7fd518dbe1c0> >

Let’s specify the objective function. We use solver.Maximize method in the case when we want to maximize the objective function and in the case of minimization we can use solver.Minimize.

# Objective function: 3x_1 + 4x_2
solver.Maximize(3 * x1 + 4 * x2)

Once we solve the problem, we can check whether the solver was successful in solving the problem using its status. If it’s successful, then the status will be equal to pywraplp.Solver.OPTIMAL.

# Solve the system.
status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print('Objective value =', solver.Objective().Value())
    print(f'(x1, x2): ({x1.solution_value():.2}, {x2.solution_value():.2})')
else:
    print('The problem does not have an optimal solution.')

Objective value = 27.5
(x1, x2): (2.5, 5.0)

36.3. Example 2: investment problem#

We now consider a problem posed and solved by [Hu, 2018].

A mutual fund has \( \$ 100,000\) to be invested over a three-year horizon.

Three investment options are available:

  1. Annuity: the fund can pay a same amount of new capital at the beginning of each of three years and receive a payoff of 130% of total capital invested at the end of the third year. Once the mutual fund decides to invest in this annuity, it has to keep investing in all subsequent years in the three year horizon.

  2. Bank account: the fund can deposit any amount into a bank at the beginning of each year and receive its capital plus 6% interest at the end of that year. In addition, the mutual fund is permitted to borrow no more than $20,000 at the beginning of each year and is asked to pay back the amount borrowed plus 6% interest at the end of the year. The mutual fund can choose whether to deposit or borrow at the beginning of each year.

  3. Corporate bond: At the beginning of the second year, a corporate bond becomes available. The fund can buy an amount that is no more than \( \$ \)50,000 of this bond at the beginning of the second year and at the end of the third year receive a payout of 130% of the amount invested in the bond.

The mutual fund’s objective is to maximize total payout that it owns at the end of the third year.

We can formulate this as a linear programming problem.

Let \(x_1\) be the amount of put in the annuity, \(x_2, x_3, x_4\) be bank deposit balances at the beginning of the three years, and \(x_5\) be the amount invested in the corporate bond.

When \(x_2, x_3, x_4\) are negative, it means that the mutual fund has borrowed from bank.

The table below shows the mutual fund’s decision variables together with the timing protocol described above:

Year 1

Year 2

Year 3

Annuity

\(x_1\)

\(x_1\)

\(x_1\)

Bank account

\(x_2\)

\(x_3\)

\(x_4\)

Corporate bond

0

\(x_5\)

0

The mutual fund’s decision making proceeds according to the following timing protocol:

  1. At the beginning of the first year, the mutual fund decides how much to invest in the annuity and how much to deposit in the bank. This decision is subject to the constraint:

    \[ x_1 + x_2 = 100,000 \]

  2. At the beginning of the second year, the mutual fund has a bank balance of \(1.06 x_2\). It must keep \(x_1\) in the annuity. It can choose to put \(x_5\) into the corporate bond, and put \(x_3\) in the bank. These decisions are restricted by

    \[ x_1 + x_5 = 1.06 x_2 - x_3 \]

  3. At the beginning of the third year, the mutual fund has a bank account balance equal to \(1.06 x_3\). It must again invest \(x_1\) in the annuity, leaving it with a bank account balance equal to \(x_4\). This situation is summarized by the restriction:

    \[ x_1 = 1.06 x_3 - x_4 \]

The mutual fund’s objective function, i.e., its wealth at the end of the third year is:

\[ 1.30 \cdot 3x_1 + 1.06 x_4 + 1.30 x_5 \]

Thus, the mutual fund confronts the linear program:

\[\begin{split} \begin{aligned} \max_{x} \ & 1.30 \cdot 3x_1 + 1.06 x_4 + 1.30 x_5 \\ \mbox{subject to } \ & x_1 + x_2 = 100,000\\ & x_1 - 1.06 x_2 + x_3 + x_5 = 0\\ & x_1 - 1.06 x_3 + x_4 = 0\\ & x_2 \ge -20,000\\ & x_3 \ge -20,000\\ & x_4 \ge -20,000\\ & x_5 \le 50,000\\ & x_j \ge 0, \quad j = 1,5\\ & x_j \ \text{unrestricted}, \quad j = 2,3,4\\ \end{aligned} \end{split}\]

36.3.1. Computation: using OR-Tools#

Let’s try to solve the above problem using the package ortools.linear_solver.

The following cell instantiates a solver and creates two variables specifying the range of values that they can have.

# Instantiate a GLOP(Google Linear Optimization Package) solver
solver = pywraplp.Solver.CreateSolver('GLOP')

Let’s create five variables \(x_1, x_2, x_3, x_4,\) and \(x_5\) such that they can only have the values defined in the above constraints.

# Create the variables using the ranges available from constraints
x1 = solver.NumVar(0, solver.infinity(), 'x1')
x2 = solver.NumVar(-20_000, solver.infinity(), 'x2')
x3 = solver.NumVar(-20_000, solver.infinity(), 'x3')
x4 = solver.NumVar(-20_000, solver.infinity(), 'x4')
x5 = solver.NumVar(0, 50_000, 'x5')

Add the constraints to the problem.

# Constraint 1: x_1 + x_2 = 100,000
solver.Add(x1 + x2 == 100_000.0)

# Constraint 2: x_1 - 1.06 * x_2 + x_3 + x_5 = 0
solver.Add(x1 - 1.06 * x2 + x3 + x5 == 0.0)

# Constraint 3: x_1 - 1.06 * x_3 + x_4 = 0
solver.Add(x1 - 1.06 * x3 + x4 == 0.0)

<ortools.linear_solver.pywraplp.Constraint; proxy of <Swig Object of type 'operations_research::MPConstraint *' at 0x7fd518dbd230> >

Let’s specify the objective function.

# Objective function: 1.30 * 3 * x_1 + 1.06 * x_4 + 1.30 * x_5
solver.Maximize(1.30 * 3 * x1 + 1.06 * x4 + 1.30 * x5)

Let’s solve the problem and check the status using pywraplp.Solver.OPTIMAL.

# Solve the system.
status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print('Objective value =', solver.Objective().Value())
    x1_sol = round(x1.solution_value(), 3)
    x2_sol = round(x2.solution_value(), 3)
    x3_sol = round(x1.solution_value(), 3)
    x4_sol = round(x2.solution_value(), 3)
    x5_sol = round(x1.solution_value(), 3)
    print(f'(x1, x2, x3, x4, x5): ({x1_sol}, {x2_sol}, {x3_sol}, {x4_sol}, {x5_sol})')
else:
    print('The problem does not have an optimal solution.')

Objective value = 141018.24349792692
(x1, x2, x3, x4, x5): (24927.755, 75072.245, 24927.755, 75072.245, 24927.755)

OR-Tools tells us that the best investment strategy is:

  1. At the beginning of the first year, the mutual fund should buy \( \$24,927.755\) of the annuity. Its bank account balance should be \( \$75,072.245\).

  2. At the beginning of the second year, the mutual fund should buy \( \$24,927.755\) of the corporate bond and keep invest in the annuity. Its bank balance should be \( \$24,927.755\).

  3. At the beginning of the third year, the bank balance should be \( \$75,072.245 \).

  4. At the end of the third year, the mutual fund will get payouts from the annuity and corporate bond and repay its loan from the bank. At the end it will own \( \$141,018.24 \), so that it’s total net rate of return over the three periods is \( 41.02\%\).

36.4. Standard form#

For purposes of

  • unifying linear programs that are initially stated in superficially different forms, and

  • having a form that is convenient to put into black-box software packages,

it is useful to devote some effort to describe a standard form.

Our standard form is:

\[\begin{split} \begin{aligned} \min_{x} \ & c_1 x_1 + c_2 x_2 + \dots + c_n x_n \\ \mbox{subject to } \ & a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n = b_1 \\ & a_{21} x_1 + a_{22} x_2 + \dots + a_{2n} x_n = b_2 \\ & \quad \vdots \\ & a_{m1} x_1 + a_{m2} x_2 + \dots + a_{mn} x_n = b_m \\ & x_1, x_2, \dots, x_n \ge 0 \\ \end{aligned} \end{split}\]

Let

\[\begin{split} A = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ & & \vdots & \\ a_{m1} & a_{m2} & \dots & a_{mn} \\ \end{bmatrix}, \quad b = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \\ \end{bmatrix}, \quad c = \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \\ \end{bmatrix}, \quad x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{bmatrix}. \quad \end{split}\]

The standard form linear programming problem can be expressed concisely as:

(36.1)#\[\begin{split} \begin{aligned} \min_{x} \ & c'x \\ \mbox{subject to } \ & Ax = b\\ & x \geq 0\\ \end{aligned} \end{split}\]

Here, \(Ax = b\) means that the \(i\)-th entry of \(Ax\) equals the \(i\)-th entry of \(b\) for every \(i\).

Similarly, \(x \geq 0\) means that \(x_j\) is greater than equal to \(0\) for every \(j\).

36.4.1. Useful transformations#

It is useful to know how to transform a problem that initially is not stated in the standard form into one that is.

By deploying the following steps, any linear programming problem can be transformed into an equivalent standard form linear programming problem.

  1. Objective function: If a problem is originally a constrained maximization problem, we can construct a new objective function that is the additive inverse of the original objective function. The transformed problem is then a minimization problem.

  2. Decision variables: Given a variable \(x_j\) satisfying \(x_j \le 0\), we can introduce a new variable \(x_j' = - x_j\) and substitute it into original problem. Given a free variable \(x_i\) with no restriction on its sign, we can introduce two new variables \(x_j^+\) and \(x_j^-\) satisfying \(x_j^+, x_j^- \ge 0\) and replace \(x_j\) by \(x_j^+ - x_j^-\).

  3. Inequality constraints: Given an inequality constraint \(\sum_{j=1}^n a_{ij}x_j \le 0\), we can introduce a new variable \(s_i\), called a slack variable that satisfies \(s_i \ge 0\) and replace the original constraint by \(\sum_{j=1}^n a_{ij}x_j + s_i = 0\).

Let’s apply the above steps to the two examples described above.

36.4.2. Example 1: production problem#

The original problem is:

\[\begin{split} \begin{aligned} \max_{x_1,x_2} \ & 3 x_1 + 4 x_2 \\ \mbox{subject to } \ & 2 x_1 + 5 x_2 \le 30 \\ & 4 x_1 + 2 x_2 \le 20 \\ & x_1, x_2 \ge 0 \\ \end{aligned} \end{split}\]

This problem is equivalent to the following problem with a standard form:

\[\begin{split} \begin{aligned} \min_{x_1,x_2} \ & -(3 x_1 + 4 x_2) \\ \mbox{subject to } \ & 2 x_1 + 5 x_2 + s_1 = 30 \\ & 4 x_1 + 2 x_2 + s_2 = 20 \\ & x_1, x_2, s_1, s_2 \ge 0 \\ \end{aligned} \end{split}\]

36.4.3. Computation: using SciPy#

The package scipy.optimize provides a function linprog to solve linear programming problems with a form below:

\[\begin{split} \begin{aligned} \min_{x} \ & c' x \\ \mbox{subject to } \ & A_{ub}x \le b_{ub} \\ & A_{eq}x = b_{eq} \\ & l \le x \le u \\ \end{aligned} \end{split}\]

\(A_{eq}, b_{eq}\) denote the equality constraint matrix and vector, and \(A_{ub}, b_{ub}\) denote the inequality constraint matrix and vector.

Note

By default \(l = 0\) and \(u = \text{None}\) unless explicitly specified with the argument bounds.

Let’s now try to solve the Problem 1 using SciPy.

# Construct parameters
c_ex1 = np.array([3, 4])

# Inequality constraints
A_ex1 = np.array([[2, 5],
                  [4, 2]])
b_ex1 = np.array([30,20])

Once we solve the problem, we can check whether the solver was successful in solving the problem using the boolean attribute success. If it’s successful, then the success attribute is set to True.

# Solve the problem
# we put a negative sign on the objective as linprog does minimization
res_ex1 = linprog(-c_ex1, A_ub=A_ex1, b_ub=b_ex1)

if res_ex1.success:
    # We use negative sign to get the optimal value (maximized value)
    print('Optimal Value:', -res_ex1.fun)
    print(f'(x1, x2): {res_ex1.x[0], res_ex1.x[1]}')
else:
    print('The problem does not have an optimal solution.')

Optimal Value: 27.5
(x1, x2): (2.5, 5.0)

The optimal plan tells the factory to produce \(2.5\) units of Product 1 and \(5\) units of Product 2; that generates a maximizing value of revenue of \(27.5\).

We are using the linprog function as a black box.

Inside it, Python first transforms the problem into standard form.

To do that, for each inequality constraint it generates one slack variable.

Here the vector of slack variables is a two-dimensional NumPy array that equals \(b_{ub} - A_{ub}x\).

See the official documentation for more details.

Note

This problem is to maximize the objective, so that we need to put a minus sign in front of parameter vector \(c\).

36.4.4. Example 2: investment problem#

The original problem is:

\[\begin{split} \begin{aligned} \max_{x} \ & 1.30 \cdot 3x_1 + 1.06 x_4 + 1.30 x_5 \\ \mbox{subject to } \ & x_1 + x_2 = 100,000\\ & x_1 - 1.06 x_2 + x_3 + x_5 = 0\\ & x_1 - 1.06 x_3 + x_4 = 0\\ & x_2 \ge -20,000\\ & x_3 \ge -20,000\\ & x_4 \ge -20,000\\ & x_5 \le 50,000\\ & x_j \ge 0, \quad j = 1,5\\ & x_j \ \text{unrestricted}, \quad j = 2,3,4\\ \end{aligned} \end{split}\]

This problem is equivalent to the following problem with a standard form:

\[\begin{split} \begin{aligned} \min_{x} \ & -(1.30 \cdot 3x_1 + 1.06 x_4^+ - 1.06 x_4^- + 1.30 x_5) \\ \mbox{subject to } \ & x_1 + x_2^+ - x_2^- = 100,000\\ & x_1 - 1.06 (x_2^+ - x_2^-) + x_3^+ - x_3^- + x_5 = 0\\ & x_1 - 1.06 (x_3^+ - x_3^-) + x_4^+ - x_4^- = 0\\ & x_2^- - x_2^+ + s_1 = 20,000\\ & x_3^- - x_3^+ + s_2 = 20,000\\ & x_4^- - x_4^+ + s_3 = 20,000\\ & x_5 + s_4 = 50,000\\ & x_j \ge 0, \quad j = 1,5\\ & x_j^+, x_j^- \ge 0, \quad j = 2,3,4\\ & s_j \ge 0, \quad j = 1,2,3,4\\ \end{aligned} \end{split}\]
# Construct parameters
rate = 1.06

# Objective function parameters
c_ex2 = np.array([1.30*3, 0, 0, 1.06, 1.30])

# Inequality constraints
A_ex2 = np.array([[1,  1,  0,  0,  0],
                  [1, -rate, 1, 0, 1],
                  [1, 0, -rate, 1, 0]])
b_ex2 = np.array([100_000, 0, 0])

# Bounds on decision variables
bounds_ex2 = [(  0,    None),
              (-20_000, None),
              (-20_000, None),
              (-20_000, None),
              (  0,   50_000)]

Let’s solve the problem and check the status using success attribute.

# Solve the problem
res_ex2 = linprog(-c_ex2, A_eq=A_ex2, b_eq=b_ex2,
                  bounds=bounds_ex2)

if res_ex2.success:
    # We use negative sign to get the optimal value (maximized value)
    print('Optimal Value:', -res_ex2.fun)
    x1_sol = round(res_ex2.x[0], 3)
    x2_sol = round(res_ex2.x[1], 3)
    x3_sol = round(res_ex2.x[2], 3)
    x4_sol = round(res_ex2.x[3], 3)
    x5_sol = round(res_ex2.x[4], 3)
    print(f'(x1, x2, x3, x4, x5): {x1_sol, x2_sol, x3_sol, x4_sol, x5_sol}')
else:
    print('The problem does not have an optimal solution.')

Optimal Value: 141018.24349792697
(x1, x2, x3, x4, x5): (24927.755, 75072.245, 4648.825, -20000.0, 50000.0)

SciPy tells us that the best investment strategy is:

  1. At the beginning of the first year, the mutual fund should buy \( \$24,927.75\) of the annuity. Its bank account balance should be \( \$75,072.25\).

  2. At the beginning of the second year, the mutual fund should buy \( \$50,000 \) of the corporate bond and keep invest in the annuity. Its bank account balance should be \( \$ 4,648.83\).

  3. At the beginning of the third year, the mutual fund should borrow \( \$20,000\) from the bank and invest in the annuity.

  4. At the end of the third year, the mutual fund will get payouts from the annuity and corporate bond and repay its loan from the bank. At the end it will own \( \$141,018.24 \), so that it’s total net rate of return over the three periods is \( 41.02\% \).

Note

You might notice the difference in the values of optimal solution using OR-Tools and SciPy but the optimal value is the same. It is because there can be many optimal solutions for the same problem.

36.5. Exercises#

Exercise 36.1

Implement a new extended solution for the Problem 1 where in the factory owner decides that number of units of Product 1 should not be less than the number of units of Product 2.

Exercise 36.2

A carpenter manufactures \(2\) products - \(A\) and \(B\).

Product \(A\) generates a profit of \(23\) and product \(B\) generates a profit of \(10\).

It takes \(2\) hours for the carpenter to produce \(A\) and \(0.8\) hours to produce \(B\).

Moreover, he can’t spend more than \(25\) hours per week and the total number of units of \(A\) and \(B\) should not be greater than \(20\).

Find the number of units of \(A\) and product \(B\) that he should manufacture in order to maximise his profit.